The Sequence Chat: Lewis Tunstall, Hugging Face, On Building the Model that Won the AI Math Olympiad
Details about NuminaMath, its architecture, training process and even things that didn't work.
Bio:
Lewis Tunstall is a Machine Learning Engineer in the research team at Hugging Face and is the co-author of the bestseller “NLP with Transformers” book. He has previously built machine learning-powered applications for start-ups and enterprises in the domains of natural language processing, topological data analysis, and time series. He holds a PhD in Theoretical Physics, was a 2010 Fulbright Scholar and has held research positions in Australia, the USA, and Switzerland. His current work focuses on building tools and recipes to align language models with human and AI preferences through techniques like reinforcement learning.
This is your second interview at TheSequence. Please tell us a bit about yourself. Your background, current role and how did you get started in AI?
I currently lead the post-training team at Hugging Face, where we focus on providing the open-source community with robust recipes to fine-tune LLMs through libraries like TRL. In a previous life, I was a theoretical physicist researching the strong nuclear force and its connection to dark matter. I accidentally stumbled into AI via my colleagues in experimental physics, who were very excited about applying a (new at the time) technique called “deep learning” to particle collisions at the Large Hadron Collider. I was surprised to learn that around 100 lines of TensorFlow could train a neural net to extract new signals from collision data, often much better than physics-derived features. This prompted me to take part in a Kaggle competition with a few physics friends, and I’ve been hooked on AI ever since!
🛠 ML Work
You were part of the team that built NuminaMath, which recently won the AI Math Olympiad. Could you tell us more about the vision and inspiration behind this project?
This project was a collaboration between Hugging Face and Numina, a French non-profit that was inspired by the AI Math Olympiad (AIMO) to create high-quality datasets and tools for the open-source community. Although there are several open weight models for mathematics, the training datasets are rarely, if ever, made public. We teamed up with Numina to bridge this gap by tackling the first AIMO progress prize with a large-scale dataset of around 850,000 math problem-solution pairs that Numina had been developing prior to the competition. We saw that winning the AIMO competition would be a great way to show the community the power of high-quality datasets and I’m very happy to see that it worked out well!
International Math Olympiads (IMO) cover a wide range of topics, from number theory to algebra and geometry. Recently, Google DeepMind published work in this area, using different models for different types of problems. Do we need specialized models for specific math disciplines, or can a single model tackle the entire set of problems?
That’s a great question and I suspect the answer will depend on how straightforward it is to integrate multiple external verifiers like Lean4 and Wolfram Alpha for models to check their proofs. The current systems are trained to interface with a single external solver, but I expect the next iteration of DeepMind’s approach will involve a generalist model that can use multiple solvers, like how LLMs currently use tools for function calling.
NuminaMath is based on the DeepSeekMath-Base model. What led you to choose this model as the baseline for math reasoning in this project?
This model was largely chosen due to the constraints of the competition: onthe one hand, only pretrained models that were released before February 2024 could be used, and on the other hand, each submission had to run on 2 T4 GPUs in under 9 hours (not easy for LLMs!). Both these constraints made DeepSeekMath 7B the best choice at the time, although there are now much better math models like those from Qwen which would likely score even better in the competition.
Could you describe the various components of the NuminaMath recipe and explain how they work together? I am particularly curious about the application of techniques such as chain-of-thought and tool-integrated reasoning.
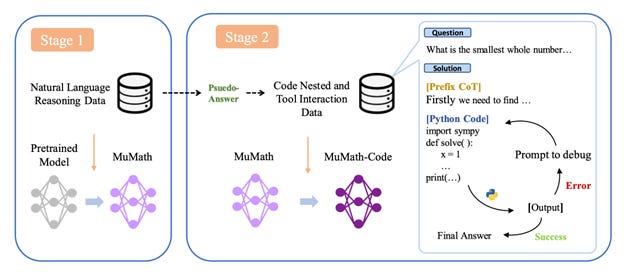
We experimented with various fine-tuning recipes, but the one that gave the best results was based on an interesting paper called MuMath-Code.
This paper combines two insights that have been shown to improve the reasoning capabilities of LLMs: Chain of Thought (CoT) templates that provide the intermediate steps needed to obtain the correct answer, and tool-integrated reasoning (TIR), where the LLM is given access to a tool like Python to run computations. Prior research had explored each one independently, but MuMath-Code showed that you get best results by performing two-stage training: first on the CoT data (to learn how to solve problems step-by-step), followed by training on TIR data (to learn how outsource part of the problem to Python). We applied this approach with DeepSeekMath 7B to the datasets Numina created and found it worked really well on our internal evals and the Kaggle leaderboard!
Do you think the NuminaMath architecture can be extended to other scientific fields, such as physics or chemistry?
Our training recipe was tailored to competitive mathematics, where one has a known answer for each problem. For competitive physics or chemistry problems, I suspect the method would generalise provided one integrates the relevant tools for the domain. For example, I suspect that in chemistry one requires access to a broad range of tools in order to solve challenging problems.
What was the training process, pipeline, and dataset for NuminaMath?
Our winning recipe was quite simple in the end and involved applying two rounds of supervised fine-tuning (SFT) to the DeepSeekMath 7B model:
Step 1: Fine-tune the base model on a dataset of 850,000 math problems, where each solution is annotatedin a CoT template.
Step 2: Fine-tune the model from Stage 1 on a synthetic dataset of tool-integrated reasoning, where each math problem is decomposed into a sequence of rationales, Python programs, and their outputs. We generated this dataset from GPT-4 to produce about 70,000 solutions.
For tools, we use the TRL library for training out models on one node of 8 x H100 GPUs. For evaluations and the Kaggle submissions we used vLLM which provides fast inference for LLMs.
What ideas did your team try but ultimately abandon during the implementation of NuminaMath?
The main ideas we tried but didn’t make it to the final submission were the following:
KTO: Using Kahneman-Tversky Optimisation (KTO) to boost the performance of our SFT models. Here the basic idea is to take your current model, generate multiple candidate solutions per problem, and then label those solutions as correct or incorrect according to the ground truth. With this data, one can then optimise the model to boost the probability it produces more of the correct versus incorrect tokens. Although we found this method worked quite well, we were unable to include it in the final submission due to various infrastructure issues on the Kaggle platform in the final days of the competition.
Model merging: We explored a variety of model merging techniques like DARE, TIES, and WARP. Here we used mergekit to merge the SFT and KTO models, or the SFT models with the public DeepSeekMath ones. Overall we found these merges led to either significant regressions on our internal evaluations and we ran out of time to explore this more deeply.
💥 Miscellaneous – a set of rapid-fire questions
What is your favorite area of research outside of generative AI?
As a former physicist, I am excited about the advances being made in AI4Science and specifically in simulating physical processes. I quite like the way Chris Bishop frames this as the “fifth paradigm” of scientific discovery and am hopeful this will help us find answers to some rather thorny problems.
Will we achieve AGI through transformers and scaling laws?
It’s always risky to predict the future, but I think it’s clear that the current systems are lacking several capabilities like episodic memory and the ability to plan over long horizons. Whether these capabilities will emerge at larger scales remains to be seen, but history generally shows that one shouldn’t bet against deep learning!
What will it take for AI to evolve from proving math theorems to formulating original theories, such as the Riemann Hypothesis or the Theory of General Relativity?
My current view is that the main barrier for models to generate novel ideas in mathematics and the natural sciences is having some means to verify correctness and compatibility with experiment. For mathematics, I suspect that projects like Lean4 will play a key role in bridging the gap from proving what is known towards generating novel theorems which are then verified automatically by the model for correctness. For the natural sciences, the challenge appears to be much harder since one needs to both synthesize vast amounts of experimental data and possibly run new experiments to validate new ideas. Nevertheless, there are already hints from works like Sakana’s AI Scientist that formulating novel ideas in ML research is possible, albeit under rather stringent constraints. It will be exciting to see how far this can be pushed into other domains!
Who is your favorite mathematician and computer scientist, and why?
My favorite mathematician is John von Neumann, mostly because I didn't really understand quantum mechanics until I read his excellent textbook on the subject.